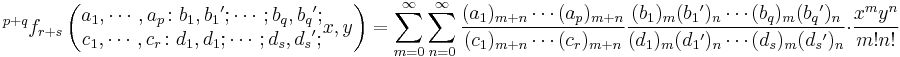Kampé de Fériet function
In mathematics, the Kampé de Fériet function is a 2-variable generalization of the hypergeometric series, introduced by Marie-Joseph Kampé de Fériet.
The Kampé de Fériet function is given by
References
- Exton, Harold (1978), Handbook of hypergeometric integrals, Mathematics and its Applications, Chichester: Ellis Horwood Ltd., ISBN 978-0-85312-122-0, MR0474684, http://books.google.com/books?id=fUHvAAAAMAAJ
- Kampé de Fériet, M. J. (1937) (in French), La fonction hypergéométrique., Mémorial des sciences mathématiques, 85, Paris: Gauthier-Villars, JFM 63.0996.03, http://books.google.com/books?id=JObuAAAAMAAJ
- Ragab, F. J. (1963). "Expansions of Kampe de Feriet's double hypergeometric function of higher order". J. f. reine angew. Mathem. (212): 113–119. doi:10.1515/crll.1963.212.113.